Home
De Gua's Theorem
18 Nov 2018
I’ve been poking around Fermat’s last theorem and specifically the relationship between that and the Pythagorean theorem. I’ll eventually get around to Fermat’s last theorem as a separate post, but I wanted to talk about de Gua’s theorem (a 3-d corollary to the Pythagorean theorem) and show you the proof I did. I only found out about de Gua’s theorem after completing the proof, because as it turns out searching “Pythagorean theorem pyramid” tends to get you geometry problems about finding the height of a pyramid. Before I tell you what de Gua’s theorem says, I’ll draw a picture of the situation.
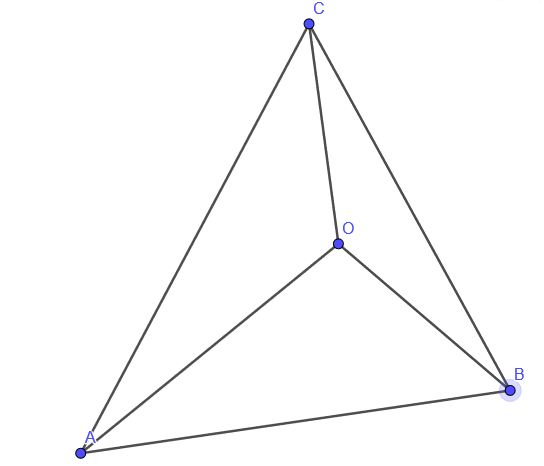
OC, OB, and OA are all at right angles to each other. De Gua’s theorem says that the sum of the squares of the area of a tetrahedron with a right angled corner is equal to the square of the area of the face that is opposite to the right angled corner. That is to say:
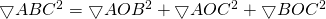
To prove this, we put a point D on the line AB, such that OD is perpendicular to AB.
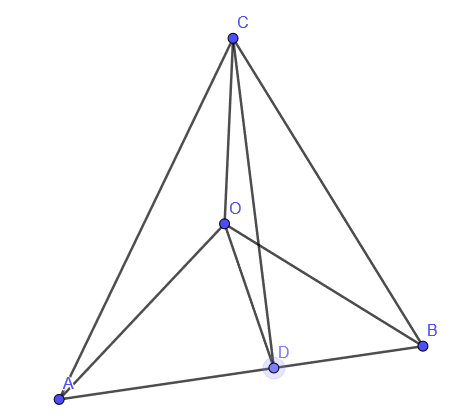
The proof starts with the fact that the length of the bottom triangle can be stated two ways, and then uses the Pythagorean Theorem to restate line segments squared as other line segments squares, and out pops de Gua’s theorem.
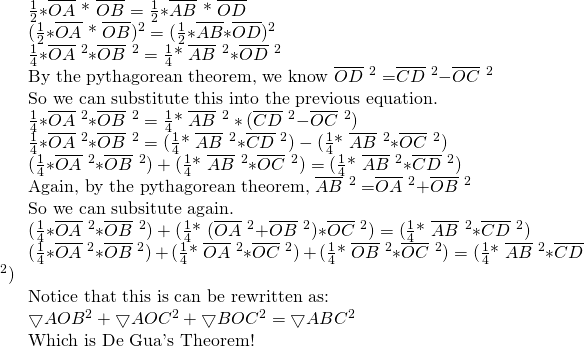
This way of stating one thing and then rewriting both sides until it meets in the middle is a very common method of solving proofs in math. If you’re interested on how this works in higher dimensions, look at Conent and Beyer’s “Generalized Pythagorean Theorem”